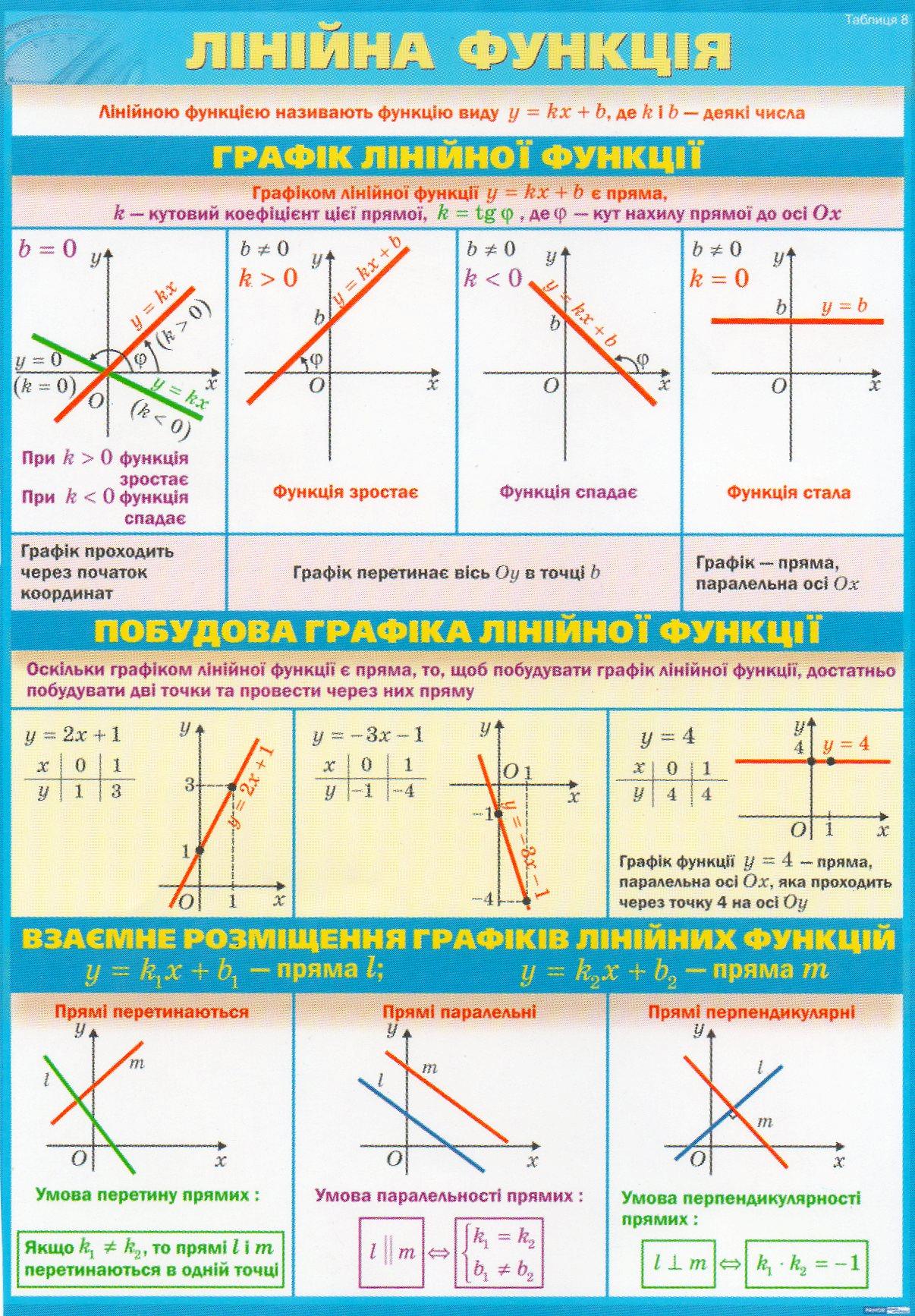
РІВНЯННЯ ПРЯМОЇ НА ПЛОЩИНІ

РІВНЯННЯ ПРЯМОЇ НА ПЛОЩИНІ

Пряма лінія в прямокутній системі координат може бути записана у  різних формах одного і того ж рівняння першого степеня. У наступних дописах переглянемо різні форми запису рівняння прямої.

Рівняння прямої

в прямокутній системі координат

з кутовим коефіцієнтом

у = kx + b,

де кутовий коефіцієнт k = tgj, кут j - це кут між прямою і додатним  напрямом осі Ох,  при цьому k, x,  b – довільні числа.


Значення х – називають аргументом, значення у – називають функцією.



Графіком лінійної функції являється пряма лінія.

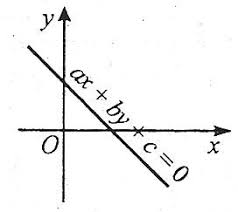
В математиці, зокрема в теорії функцій це рівняння задає так звану  лінійну функцію, графіком  якої в прямокутній системі координат є пряма лінія.  І навпаки, будь-яка пряма лінія в прямокутній системі координат може бути записана у вигляді ax+by+c=0.



В арифметиці чисел  рівнянням 
у = kx + b 
задають послідовність чисел, яку називають арифметична прогресія, зрозуміло, що  k, b – довільні числа,  х – натуральні числа(номер члена прогресії).  
У фізиці  рівняннями 
у = kx + b 
задають  або описують рівномірні процеси, наприклад, рівномірний рух  транспорту по прямій. 
А в теорії цілих чисел рівняннями 
у = kx + b  
задають  послідовність чисел, які при ділення на ціле k мають остачу  b, (зрозуміло, що k – дільник числа у, b – остача,  х – неповна частка).

Рівняння прямої, що проходить через дві задані точки

Арифметична прогресія і рівняння прямої.

1.  Числова послідовність, кожен член якої, починаючи з другого, дорівнює попередньому члену, складеному з одним і тим же числом, називається арифметичною прогресією.
Приклад:  1) 3,7;.....;   2) -5, -1,.......
2.  Різниця між будь-якими двома сусідніми членами арифметичної прогресії дорівнює одному і тому ж числу.
Приклад:  3, 7, 11, 15, 19, ............
                    7-3=4; 11-7=4; 15-11=4; 19-15=4; .......
Це число називається різницею арифметичної прогресії та позначається буквою d.
Приклад:  3,7,11,15,19,......; d=4.

Арифметична прогресія може бути записана у вигляді формули:
 у = kx + b.

Приклади: 1) якщо k = 0, b = 0, то

у = 0

 - це рівняння вісі абсцис Ох;

2) якщо k = 0, b ≠ 0, то

у = b

 - це рівняння прямих, що паралельні до осі  абсцис і проходять через точку (0;  b);

3) якщо k = 1, b = 0, то

у = х

- це рівняння  прямої, що є бісектрисою першої  та третьої координатних чвертей);

4) якщо k = -1, b = 0, то

у = - х

 - це рівняння  прямої, що є бісектрисою другої  та чевертої координатних чвертей);

5) якщо k = 2, b = 0,  х = n – цілі числа, то

у = 2n

- це рівняння  парних чисел;

6) якщо k = 2, b = -1,  х = n – цілі числа, то

у = 2n-1

- це рівняння  непарних чисел;

7) якщо k = 6, b = -1,  х = n – цілі числа, то

у = 6n-1

 - це рівняння  цілих чисел, які при діленні на 6 дають остачу 5;

8) якщо k = 6, b = +1,  х = n – цілі числа, то

у = 6n+1

- це рівняння  цілих(непарних) чисел, які при діленні на 6 дають остачу 1;

9) якщо k = 15, b = +1,  х = n – цілі числа, то

у = 15n+1

 - це рівняння  цілих(парних і непарних) чисел, які при діленні на 3 і на 5 дають остачу 1.

Завдання для самостійного дослідження.

1.     Які умови треба накласти на k і b у рівнянні прямої у = kx + b, щоб  цілі значення у були:

·        кратними 4;

·        тільки парними, що діляться на 7;

·        тільки непарними, що діляться на 9?

2.     Периметр прямокутника зі сторонами х дм і 8 дм дорівнює Р дм. Запишіть формулу лінійної залежності Р від х.

3.     Знайдіть значення аргументу, при якому:

a.       функція у = kх набуває значення  у ={ -8; 0; 12}

b.       функція у  = 4х + b набуває значення  у = {-1; 3; 17}.

4.    Пряма у = kх + b проходить через точку А(-2; 22)
і паралельна прямій у = 2 - х. Знайдіть значення k і b.

5.     На початку нагрівання вода мала температуру 20 . При нагріванні температура води підвищувалася щохвилини на 5 .

·        Задайте формулою залежність температури y води від часу x і її нагрівання.

·        Знайдіть значення  y, що відповідає значенню аргу­менту  7; 9; 10.

·        Знайдіть значення x, яким відповідає  45; 60; 70.

·        При якому значенні x і вода закипить?

6.    Побудувати рівняння прямих в прямокутній системі координат:

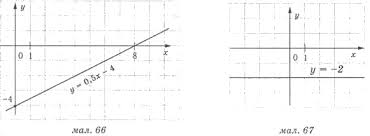
а) у = - 2х + 3; б) у = 0,5х – 4; в) у =  + 2х – 3.              

Знайти усі координати точок перетину трьох прямих. Який вид трикутника задають ці прямі?

6. Побудувати графіки функцій

a) у = - х – 3; б)  у = + х + 4;   в) у =  – х + 4;  г)  у =  + х - 3.

Знайти усі координати точок перетину чотирьох прямих. Який вид чотирикутника задають ці прямі?

Які точки  А(-5; 4), В(0; -4), С(0; -1)  лежать в середині чотирикутника?

7.  Рівняння прямих задано такими формулами:

a.       у = -3 – x; 

b.      у = - 5 + 2х;

c.       у = -3х – 4;

d.      у =  – 0,5х -2,4;

Заповніть таблицю в зошиті, обчисливши відповідні значення та аргументи лінійної функції у = kх + b.

х	-3		-1		1		3
у		-2		0		2

8. Пряму лінію  у = kх + b задано таблицею. Знайдіть: 

1) значення лінійної функції, якщо х = {-4; 0; 1}; 

2) значення аргументу, при якому значення функції y = {-3; -2; 7}; 

3) область визначення функції; 

 4) область значень функції.

х	-3	-2
у	-9	-7