Квадратична функція та її графік.

Квадратична функція та її властивості.

Означення. Функції вигляду f(x) = ax² + bx + c називається квадратичною, якщо a -  ненульове дійсне число, b, с – дійсні числа.

Застосування квадратичної функції в економіці:

Графіком квадратичної функції у = ax² + bx + c  є крива лінія, яку називають квадратичною  параболою.

Приклад

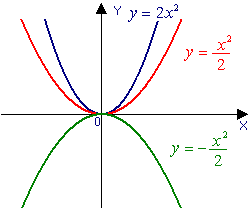
Дискримінант D = b² – 4ac, 

Нулі квадратичної функції:  

х₁ = (‒ b ‒ (b² ‒ 4ac)^0,5 )/(2a),

х₂ = (‒ b + (b² ‒ 4ac)^0,5 )/(2a).

ТРИ способи  запису  квадратичної функції:

у (x) = f(x)= ax² + bx + c = а(х – х₁)(х – х₂)= а(х -0,5b:a)² – 0,25D:a.

Координати вершини  квадратичної  параболи: 

х_в = - 0,5b:a;  у_в =  - -0,5b:a.

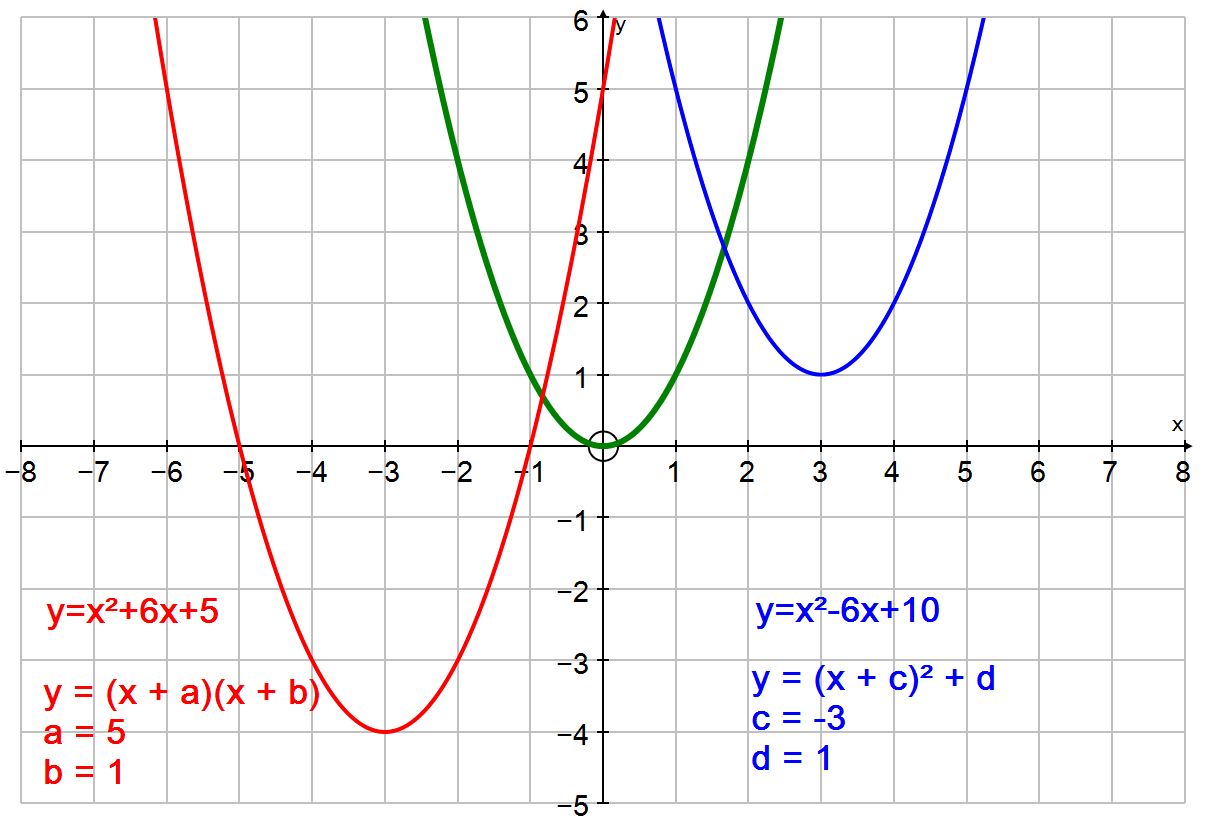
Приклад. Графік квадратичної функції задано формулою:

f(x) = ax² + bx + c.

Знайти усі нулі параболи, вершину параболи та коефіцієнти a,  b,  c, якщо відомо, що

f(1) =  2010;  f(–1) =  0.

Розв’язання.

 Знайдемо значення функції при х = 1.

f(1) =  a×1² + b×1 + c = a + b + c  = 2010.

Таким чином, отримаємо.

a + b + c  = 2010,             (1)

Знайдемо нульове значення функції при х = -1.

f(–1) = a×(–1)² + b×(–1) + c = a – b + c  = 0,

 звідси випливає  рівність

b = a + с .             (2).

Вираз (2) підставимо у ліву частину виразу (1) замість суми а + с, отримаємо:

b + a + c  = b + b  = 2010,

2×b  = 2010,

b = 1005.              (3)

Зазначимо, що х₁ = –1 – нуль функції, тобто, -1 – це корінь рівняння

ax² + bx + c = 0.

У цього квадратного рівняння існує і другий корінь. Знайдемо  х₂.

Використовуючи  теорему Вієта, запишемо суму коренів:

  х₁ + х₂ = –  b/а = – 1005.       (4)

Знаючи, перший корінь х₁ = –1  і  b = 1005, маємо два рівняння:             

–1 + х₂ = – 1005.

–  1005/а = – 1005.      

Звідси, отримаємо старший коефіцієнт 

а = 1

та другий корінь:

х₂ = – 1004.

Таким чином, маємо два нулі параболи: х₁ = –1, х₂ = – 1004.

Вкажемо ще один спосіб знаходження значення старшого коефіцієнта а за допомогою  двох нулі і абсциси вершини параболи.

Квадратична парабола є симетричною відносно прямої

у = – 0,5b/а.

 Тому  нулі х₁ , х₂ параболи  – це симетричні точки на осі Ох відносно точки х_в =  – 0,5b/а. Таким чином,  х_в =  – 0,5b/а – це середина відрізка, кінцями якого являються нулі параболи. Середину відрізка можна знайти за формулою:

х_в =  0,5(х₁ + х₂)  = – 0,5b/а.

Враховуючи рівність (3) та (4), маємо

х_в =  0,5(х₁ + х₂)  = 0,5×(-1005)  = –502,5 = – 0,5×1005/а.

Отримали рівняння:

502,5 = – 0,5×1005/а.

Звідси, отримуємо  старший коефіцієнт:  а = 1.

Знайдемо вільний  член с.

Використовуючи  теорему Вієта запишемо добуток коренів:

  х₁×х₂ = с/а = с:1 = с.      

Тобто, вільний член

                          с =  х₁×х₂ = -1×(–1004) = 1004.

Остаточно,  а = 1,  b = 1005, с = 1004.            

Дії з квадратними тричленами

Означення. Два квадратні тричлени

f(x) = а₁х² + b₁x + c₁  

та  

 g(x) = а₂х² + b₂x + c₂

 рівні, якщо рівні їхні коефіцієнти при х², рівні їхні коефіцієнти при х і вільні члени обох тричленів теж рівні, тобто якщо

а₁ = а₂,

b₁ = b₂,

c₁ = c₂,

то 

f(x) = g(x).

Дії з квадратними тричленами.

Означення. Сумою двох  квадратних тричленів

f(x) = а₁х² + b₁x + c₁  

 та   

g(x) = а₂х² + b₂x + c₂

називають третій квадратний тричлен,

s(x) = f(x) +  g(x) = S₂х² + S₁x + S₀

коефіцієнти якого отримують  додаванням відповідних коефіцієнтів при  х²,  при х і  вільний член(при х⁰) отримують   додаванням обох вільних членів даних тричленів, тобто

S₂ =  а₁ + а₂,

S₁ =  b₁ + b₂,

S₀ =  c₁ + c₂.

Означення. Добутком двох  квадратних тричленів

f(x) =  а₁х² + b₁x + c₁

та

g(x) = а₂х² + b₂x + c₂

 називають  многочлен четвертого степеня

p(x) = f(x)g(x) = P₄х⁴ + P₃x³ + P₂х² + P₁x + P₀,

 коефіцієнти якого, отримують із коефіцієнтів квадратних тричленів за правилами:

P₄ = а₁а₂ 

P₃ = а₁b₂ + а₂b₁

P₂ = а₁c₂ + а₂c₁ + b₁b₂

P₁ = c₂b₁ + c₁b₂

P₀ = c₁c₂

Алгоритм ділення многочленів з остачею

Для будь-яких многочленів

f(x) = а₁х² + b₁x + c₁  

 та   

g(x) = b₂x + c₂

існує частка

q(x)

 і такі, що

f(x)=g(x)q(x)+r(x),

при цьому степінь r(x) менше степені

g(x) або  r(x) = 0.

Многочлени g(x) і r(x) визначені однозначно.

Частку і остачу  знаходять за допомогою письмового ділення «куточком».

 

Дільники многочлена

Означення. Дільник квадратного тричлена f(x) – це лінійний або 

квадратний многочлен, g(x), такий, що

f(x) = g(x)q(x).

         Означення. Найбільший спільний дільник многочленів f(x) и g(x) - такий їх спільний дільник d(x), який делиться на довільний другий їх спільний дільник.

Інтерполяційна формула Лагранжа

для квадратного тричлена

Дано три точки

(x₁; у₁),  (x₂; у₂), (x₃; у₃).

невідомого квадратного тричлена

ах² + bx + c,

тоді можна записати квадратний тричлен за допомогою формули Лагранжа:

f(x) = ах² + bx + c =

= y₁(x-x₂) (x-x₃)/(x₁ –x₂)(x₁ –x₃) +

+ y₂(x-x₁) (x-x₃)/(x₂ – x₁)(x₂ –x₃) +

+ y₃(x-x₂) (x-x₁)/(x₃ –x₁)(x₃ -x₂)

Приклад. Знайти коефіцієнти квадратного тричлена і записати його в стандартному вигляді, якщо відомі абсциси і ординати тільки для трьох точок: x₁ = 1; x₂ = 3; x₃ = 4; y₁ = 2; y₂ = -2; y₃ = -1.

Розв’язання. Скористаємося інтерполяційною формулою Лагранжа для квадратного тричлена:

f(x) = ах² + bx + c =  y₁(x-x₂) (x-x₃)/(x₁ –x₂)(x₁ –x₃) + y₂(x-x₁) (x-x₃)/(x₂ – x₁)(x₂ –x₃) + y₃(x-x₂) (x-x₁)/(x₃ –x₁)(x₃ -x₂) =

= 2(x-3)(x-4)/(1 –3)(1 – 4) - 2(x-1)(x-4)/(3 – 1)(3 –4) -1(x-3)(x-1)/(4 – 1)(4 -3) = х² - 6x + 7.

Приклад. Дано графіки квадратичної  функції

f(x) = ax²+ bx+ c, де ненульове число a¹

та лінійної  функції 

g(x) = kx+l

в прямокутній системі координат хОу.

Чи можна за допомогою циркуля та лінійки виконати побудову  різниці графіків  f(x) - g(x)?

Розв’язання. Якщо утворити різницю

R(x) = f(x) - g(x) = ax²+ bx+ c – kx - l  = ax²+ (b-k)x + (c-l),

то отримаємо квадратичну функцію R(x), у якої на відмінну від квадратичної функції f(x) змінилися параметри лінійної частини.  

Зазначимо такі властивості параметрів квадратичної функції.

1.    При зміні параметра а ( параметри b та  c не змінюються) в формулі квадратичної функції, графік параболи деформується прямокутній системі координат хОу  відносно власної осі симетрії(вітки параболи звужуються (½а½> 1  ) до осі симетрії, або розтягуються (½а½£ 1  )  від осі симетрії).

2.     При додатному значенні параметра а – обидві вітки квадратичної параболи напрямлені вгору. При від’ємному значенні параметра а – обидві  вітки квадратичної параболи напрямлені вниз.

3.    При зміні двох лінійних параметрів b та  c ( параметр  а    не змінюються) квадратичної функції f(x) = ax²+ bx+ c в прямокутній системі координат хОу  переміщується вісь симетрії параболи(графік не деформується по відношенню до власної осі симетрії),  тобто,  переміщується  вершина ( Х_f; Y_f ) параболи

f(x) = ax²+ bx+ c

в нову вершину ( Х_r; Y_r )  параболи

R(x) = ax²+ (b-k)x + c-l.

Знайдемо координати вершини ( Х_f; Y_f ) параболи f(x) = ax²+ bx+ c:

Х_f = - b/(2a);

Y_f = a(- b/(2a)  )²+ b(- b/(2a)  )+ c = -b²/4a + c.

Знайдемо координати вершини ( Х_r; Y_r )  параболи R(x) = ax²+ (b-k)x + (c-l) та дізнаємося як перемістилися ці координати в прямокутній системі координат хОу по відношенню до вершини ( Х_f; Y_f ):

Х_r=( k- b)/(2a) = Х_f + k/2a;

Y_r = a(( k- b)/(2a))²+ (b –k) (( k- b)/(2a))+ c- l =

=  -(b-k)²/4a + c-l= (- b²+ 2bk - k²)/4a    + c- l =

= Y_f +(2bk - k²)/4a   - l .

Звідси отримали таке переміщення двох вершин  парабол:

( Х_r; Y_r ) ® (Х_f + k/2a ; Y_f +(2bk - k²)/4a   - l ).

За властивістю переміщення можна рухати не вершину ( Х_f; Y_f ) параболи f(x) = ax²+ bx+ c, а осі   координат. Отже, досить циркулем та лінійкою виконати паралельне перенесення координатних осей в точку

                                      (-k/2a;  - (2bk - k²)/4a   - l ).

Відповідь: можна.

Квадратичну функцію можна записати у параметричній формі:

f(x) = ах² + bx + c =  а(х ‒ т)² + b(х ‒ т) +  c + 2аmx  ‒ аm² + bm

f(x) = ах² + bx + c =  а(х ‒ 0,5b:a)² + b(х ‒ 0,5b:a) +  c ‒ 0,25b²:a

f(x) = ах² + bx + c =  а(х ‒ х₁)² + b(х ‒ х₁) +  2ах₁x 

ВЛАСТИВОСТІ КВАДРАТИЧНОЇ ФУНКЦІЇ. МАТЕМАТИЧНИЙ ДИКТАНТ.

Вважайте, що запитання коректні і правильні.  Відкорегуйте  деякі  відповіді.

1.     Які форми запису існують у квадратичної функцій? Запишіть їх у свій зошит і перенумеруйте.

Відповідь: у = ах²+ bх +c = а(х-m)²+ n = а(х-x₁)(х-x₂).

2.     Як називаються  графіки  квадратичних функцій?  За скількома точками графіка можна відновити формулу  квадратичної функції.

Відповідь: Квадратичні параболи. За довільними трьома точками.

3.     Яку властивість симетрії мають  квадратичні функції? Як цю симетрію знайти на графіку?

Відповідь: Осьову симетрії мають квадратичні параболи. Осьовa симетрія квадратичної параболи  задається рівнянням прямої: х = -b/(2a).

4.     Як можна знайти число, яким обмежений графік квадратичної функції?

Відповідь: Знайти координати вершини параболи за формулою(-b/(2a);  –D/ (4a)  ). Якщо а>0,  то графік обмежений знизу числом –D/ (4a) і необмежений зверху. Якщо  a<0, то графік обмежений зверху числом  –D/ (4a) і необмежений знизу.

5.     Як можна знайти координату точки перетину графіку квадратичної параболи та вісі ординат  Оу?

Відповідь: координата точки перетину квадратичної параболи з Оу – це (0; с), де с – вільний член у формулі  у=ах²+ bх +c. Або  зробити так: у формулу у = ах²+ bх +c  підставити замість аргументу х значення нуль і обчислити утворений вираз. 

6.      Як знайти, скільки може  мати нулів квадратична функція на множині дійсних чисел?

Відповідь: Можна зробити це так: у формулу  у = ах²+ bх +c  підставити замість змінної у значення нуль і розв’язати квадратне рівняння, кількість розв’язків  рівняння вказує на кількість нулів функції. Або обчислити  знак дискримінанту  D = b² – 4ac квадратного рівняння: якщо від’ємний b² – 4ac<0, то функція нулів немає (парабола не перетинає вісь Ох), якщо нульовий  b² – 4ac =0 , то нуль функції тільки один(парабола тільки дотикається вісі Ох),  якщо додатний  b² – 4ac >0 , то у функції нулів аж два(парабола перетинає вісь Ох у двох точках). Взагалі, зрозуміло, що на графіку параболи нулі функції – це значення саме  абсциси х, в яких  графік  параболи перетинає вісь абсцис Ох.

Якщо знайдена або відома форма запису формули квадратичної функції у вигляді множників  у= а(х-x₁)(х-x₂), то функція має два нулі:  х₁,  х₂.  Якщо знайдена форма запису формули квадратичної функції у вигляді множників  у= а(х-x₁)², то один нуль: х₁.  Якщо  вираз  ах²+ bх +c  на лінійні множники не розкладається на множині дійсних чисел, то квадратична функція  у = ах²+ bх +c  немає нулів на множині дійсних чисел.

7.     Як можна знайти координати вершини параболи?

Відповідь: Можна зробити це так:   (-b/(2a);  –D/ (4a))  або  знайти два числа за такими формулами:  х_в = -b/(2a);   у_в = ах_в ²+ bх_в +c.

8.       Як можна знайти координати вершини параболи у формулі: у = а(х - m)² + n?

Відповідь: Можна записати  координати вершини параболи так:  (m; n).

ВЛАСТИВОСТІ КВАДРАТИЧНОЇ ФУНКЦІЇ. МАТЕМАТИЧНИЙ ДИКТАНТ.

Вважайте, що запитання коректні і правильні.  Відкорегуйте  деякі  відповіді.

9.      Як треба  використовувати знак найстаршого коефіцієнта, щоб дізнатися розташування графіка квадратичної функції?

Відповідь:  Якщо додатний знак а>0,  то  парабола з вітками вгору, графік обмежений знизу числом –D/ (4a) і необмежений зверху.  Якщо  від’ємний знак a<0, то парабола з вітками вниз,  і графік обмежений зверху числом  –D/ (4a) і необмежений знизу.

10.             Як можна знайти  проміжки,  де  квадратична функція додатна?

Відповідь:  Якщо квадратична функція додатна на проміжку (а; b),  то графік на цьому проміжку лежить тільки вище осі Ох. А взагалі треба розв’язати квадратну нерівність ах²+ bх +c >0 довільним способом.  Розв’язок цієї нерівності і буде шуканим проміжком.

11.           Як можна знайти  проміжки, де  квадратична функція від’ємна?

Відповідь:  Якщо квадратична функція від’ємна на проміжку (а; b),  то графік на цьому проміжку лежить тільки нижче осі Ох. А взагалі треба розв’язати квадратну нерівність ах²+ bх +c <0 довільним способом.  Розв’язок цієї нерівності і буде шуканим проміжком.  

12.           Як можна знайти  проміжки,  де  квадратична функція недодатна?

Відповідь:  Якщо квадратична функція недодатна на проміжку [а; b],  то графік на цьому проміжку лежить не вище осі Ох. А взагалі треба розв’язати квадратну нерівність ах²+ bх +c ≤ 0 довільним способом.  Розв’язок цієї нерівності і буде шуканим проміжком.

13.           Як можна знайти  проміжки, де  квадратична функція невід’ємна?

Відповідь:  Якщо квадратична функція невід’ємна на проміжку [а; b],  то графік на цьому проміжку лежить тільки нижче осі Ох. А взагалі треба розв’язати квадратну нерівність ах²+ bх +c ≥ 0 довільним способом.  Розв’язок цієї нерівності і буде шуканим проміжком.

14.            Як можна знайти  проміжки, де  квадратична функція зростає?

Відповідь:  Побудувати ескіз графіка квадратичної функції і за графіком визначити проміжок зростання.  Якщо а>0,  то функція зростає на проміжку  [-b/(2a);  +оо),  . Якщо  a<0, то то функція зростає на проміжку  ( -оо;  -b/(2a)].

15.           Як можна знайти  проміжки, де  квадратична функція спадає?

Відповідь:  Побудувати ескіз графіка квадратичної функції і за графіком визначити. Якщо а<0,  то функція спадає на проміжку  [-b/(2a);  +оо) .  Якщо  a>0, то функція cпадає на проміжку  ( -оо;  -b/(2a)].

16.            Як можна знайти  проміжки, де  квадратична функція у = ах²+ bх +c  не існує?

Відповідь:  Квадратична функція  у = ах²+ bх +c визначена в усіх точках. Тому проміжків, де не визначена квадратична функція  не існує. Або побудувати ескіз графіка квадратичної функції і за графіком визначити.

17.             Як можна знайти  точки, де  квадратична функція має екстремум?

Відповідь:  Якщо  a<0, то функція  не має найменшого значення, тобто  мінімуму, але має точку максимуму  х_мах = -b/(2a), та максимальний екстремум: у_мах = –D/ (4a).  Якщо  a>0, то не має найбільшого значення, тобто максимуму, але має  функція  має точку мінімуму  х_min= -b/(2a), та мінімальний екстремум: у_min = –D/ (4a).  

Приклад. Дано графіки квадратичної  функції

f(x) = ax²+ bx+ c, де a¹0

та лінійної  функції 

g(x) = kx+l

в прямокутній системі координат хОу.

Чи можна за допомогою циркуля та лінійки виконати побудову  різниці графіків  f(x) - g(x)?

Розв’язання. Якщо утворити різницю

R(x) = f(x) - g(x) = ax²+ bx+ c – kx - l  = ax²+ (b-k)x + (c-l),

то отримаємо квадратичну функцію R(x), у якої на відмінну від квадратичної функції f(x) змінилися параметри лінійної частини.  

Зазначимо такі властивості параметрів квадратичної функції.

1.    При зміні параметра а ( параметри b та  c не змінюються) в формулі квадратичної функції, графік параболи деформується прямокутній системі координат хОу  відносно власної осі симетрії(вітки параболи звужуються (½а½> 1  ) до осі симетрії, або розтягуються (½а½£ 1  )  від осі симетрії).

2.     При додатному значенні параметра а – обидві вітки квадратичної параболи напрямлені вгору. При від’ємному значенні параметра а – обидві  вітки квадратичної параболи напрямлені вниз.

3.    При зміні двох лінійних параметрів b та  c ( параметр  а    не змінюються) квадратичної функції f(x) = ax²+ bx+ c в прямокутній системі координат хОу  переміщується вісь симетрії параболи(графік не деформується по відношенню до власної осі симетрії),  тобто,  переміщується  вершина ( Х_f; Y_f ) параболи

f(x) = ax²+ bx+ c

в нову вершину ( Х_r; Y_r )  параболи

R(x) = ax²+ (b-k)x + c-l.

Знайдемо координати вершини ( Х_f; Y_f ) параболи f(x) = ax²+ bx+ c:

Х_f = - b/(2a);

Y_f = a(- b/(2a)  )²+ b(- b/(2a)  )+ c = -b²/4a + c.

Знайдемо координати вершини ( Х_r; Y_r )  параболи R(x) = ax²+ (b-k)x + (c-l) та дізнаємося як перемістилися ці координати в прямокутній системі координат хОу по відношенню до вершини ( Х_f; Y_f ):

Х_r=( k- b)/(2a) = Х_f + k/2a;

Y_r = a(( k- b)/(2a))²+ (b –k) (( k- b)/(2a))+ c- l =

=  -(b-k)²/4a + c-l= (- b²+ 2bk - k²)/4a    + c- l =

= Y_f +(2bk - k²)/4a   - l .

Звідси отримали таке переміщення двох вершин  парабол:

( Х_r; Y_r ) ® (Х_f + k/2a ; Y_f +(2bk - k²)/4a   - l ).

За властивістю переміщення можна рухати не вершину ( Х_f; Y_f ) параболи f(x) = ax²+ bx+ c, а осі   координат. Отже, досить циркулем та лінійкою виконати паралельне перенесення координатних осей в точку

                                      (-k/2a;  - (2bk - k²)/4a   - l ).

Відповідь: можна.

Довідник. Формули скороченого множення

Властивості степенів з цілим показником

аⁿa^m=a^n+m;  аⁿ:a^m=a^n-m;  (аⁿ)^m=a^nm;  а⁰=1;  а^-n=1:aⁿ; а=а^0,5a^0,5=1a¹ =(a^0,5)²;

(ab)^m = a^mb^m = 1/a^{– m}b^{– m} =(ab)^m;     a^m:b^m = (a:b)^m = b^{– m} a^{– m} =(b:a) ^{– m}       

 Різниця та сума квадратів    1=0,25(m²+1)² – 0,25(m²-1)² ;  m=(m+0,25)²-(m-0,25)² ;   m²=0,25(m²+1)²-0,25(m²-1)²;   mⁿ=0,25(mⁿ+1)²-0,25(mⁿ-1)²   

a² + b² – не розкладається  на цілі множники на множині многочленів

a² – b² = (a – b)(a + b) – це різниця квадратів двох виразів.

Різниця та сума кубів

а³ – b³ = (a – b)(a² + аb + b²) – це різниця кубів двох виразів.

а³ + b³ = (a + b)(a² – аb + b²) – це cума кубів двох виразів.

Різниця та сума біквадратів

а⁴ – b⁴ = (a – b)(a³ + а²b + аb² + b³) = (a – b)(a + b)( a² + b²);

а⁴ + b⁴  - не розкладається на множники

а⁵ – b⁵= (a – b)(a⁴+ а³b + а²b² + аb³ + b⁴);

а⁵ + b⁵= (a+b)( a⁴ – а³b + а²b² – аb³ + b⁴);

a^2m + b^2m  - не розкладається на множники

аⁿ – bⁿ = (a–b)( a^n-1+ а^n-2b + а^n-3b² +… + а²b^n-3 + аb^n-2 + b^n-1);

Якщо  b =1, тоді  аⁿ – 1= (a–1)( a^n-1+а^n-2  + а^n-3  +… +а² + а + 1);

Степінь суми двох виразів.

(a±b)⁰ = 1;        (a±b)¹ = a±b;  1:aⁿ ±(1:bⁿ) =a^-n±b^-n=(ab)^-n(aⁿ ± bⁿ) =a^-n ± b^-n 

Квадрат  двочлена:

(a + b)² =(b + a)² = a² + 2ab + b² –  це квадрат суми двох чисел.

(a – b)² =(b – a)² = a² – 2ab + b² –  це квадрат різниці двох чисел.

Куб  двочлена:

(a + b)³ = a³ + 3a²b + 3ab² + b³  – це куб суми двох чисел;

(a – b)³ = a³ – 3a²b + 3ab² – b³  – це куб суми або різниці двох чисел;

Іноді стають у нагоді такі формули:

(a±b)⁴ = a⁴±4a³b +6a²b² ±4ab² + b⁴;

(a±b)⁵ = a⁵±5a⁴b +10a³b² ±10a²b³ +5ab⁴ ± b⁵;

(a±b)⁶= a⁶±6a⁵b +15a⁴b² ±20a³b³ +15a²b⁴ ±6ab⁵ +b⁶.

Для непарних n: аⁿ + bⁿ = (a+b)( a^n-1-а^n-2 b + а^n-3b² -… +а²b^n-3 - аb^n-2 + b^n-1);

Якщо  b =1, тоді a²ⁿ⁺¹ + 1= (a+1)( a^n-1- а^n-2  - а^n-3  +… +а² - а + 1);

Сума трьох квадратів і трьох кубів.

а³ + b³ + c³ - 3abc = (a+b+c)(a² + b² +c² –аb–bc–ac);

(a + b + c)² = a² + b² + c² + 2аb + 2bc +2ac;

(a – b)³ + (b – c)³ + (c – a)³ =3 (a – b)(b – c)(c – a).

a⁴ + 4 =  (a² – 2a + 2)(a² + 2a + 2);

a⁴ + a² + 1 = (a² + a + 1)(a² – a + 1);

а⁵ + a +1 = (a² + a + 1)(a³ – a² + 1);

a¹⁰ + a⁵ + 1 = = (a² + a + 1)(a⁸ – a⁷ + a⁵ – a⁴ + a³ – a + 1);

a³ + b³ + c³ – 3abc = (a + b +  c)(a²+ b² + c² – ab – ac – bc).

a⁴ + 4b⁴ = (a² – 2ab + 2b²)(a² + 2ab + 2b²);

4a⁴ + b⁴ =  (2a² – 2ab + b²)(2a² + 2ab + b²);

(х – m)(х – m - 2) + 1 = (х – m - 1)²;

1+ (n-1)n(n+1)(n+2)=(n²+n-1)²;

 (х-а)(х-(а+1))(х-(а+2))(х-(а+3))+1 = ((х²-(а +4)х+ (а+4))²;

 16+(n-2)n(n+2)(n+4)=(n² + 2n- 4)² ;  

81+(n-3)n(n+3)(n+6)=(n² + 3n- 9)²; 

256+(n-4)n(n+4)(n+8)=(n² + 4n- 16)²;

k⁴+(n-k)n(n+k)(n+2k)=(n² + kn- k²)²;

k⁴+(n+k)(n+2k)(n+3k)(n+4k)=(n² + 5kn+5k²)²; 

 якщо m+k=p+q, тоді

 |mkpq-(0,5km+0,5pq)²|+(x+k)(x+m)(x+p)(x+q))=

=(x² - (k+m)x+0,5km+0,5pq)²; 

 Три способи запису квадратного тричлена

ax² + bx + c = а(х – х₁)(х – х₂)= а(х - 0,5b:a)² – 0,25D:a.

Запис квадратного тричлена у вигляді декількох квадратів:

ax² + bx + c=m(x-k)²+p(x-q)²

ax² + bx + c=m(x-k)²+p(x-q)² +u(x-v)² 

Дискримінант  D = b² – 4ac. 

Два корені:   х₁ = (‒ b ‒ (b² ‒ 4ac)^0,5 )/(2a),  х₂ = (‒ b + (b² ‒ 4ac)^0,5 )/(2a).  

Розв’язування квадратного рівняння без обчислень дискримінанта:

Якщо a + b + с = 0, то корені  кв. рівняння:  х₁ = 1,  х₂ = с/а.  

Якщо а - b + с = 0, то корені кв. рівняння:   х₁ = - 1,  х₂ =  - с/а.  

Координати вершини  квадратичної  параболи  y= ax² + bx + c

це точка (х_верш; у_верш), де х_верш= - 0,5b:a =0,5(х₂ + х₁);    

 у_верш =  aх_верш ²+ bх_верш+c= -D/4a.

x² + 2ax + b =  n₁(x + m₁)² + n₂(x + m₂)² + n₃(x + m₃)²

xy + x + y  + а = (х + 1)(y + 1) + а - 1_.                xy + x + y  + 1= (х + 1)(y + 1)

aху + bх + cу + d = (x + c:a)(ау + b) + d – (cb:a).

Якщо b² ‒ 4ac – невід’ємний,  то ax² + byх + cy² = а(х ‒ k₁y) (х ‒ k₂y),

де k₁, k₂ ‒ корені квадратного рівняння  ak² + bk + c = 0.

А) многочлен (х - а₁) (х - а₂)(х - а₂) … (х -  а_n) - 1 – незвідний, тобто не розкладається на многочлени меншого степеня, якщо а_і  – різні числа

Б) многочлен (х - а₁)(х - а₂)(х - а₂) … (х -  а_n) + 1 – незвідний, тобто не розкладається на многочлени меншого степеня, окрім наступних випадків:

1+ (n-1)n(n+1)(n+2)=(n²+n-1)²;

 (х-а)(х-(а+1))(х-(а+2))(х-(а+3))+1 = ((х²-(а +4)х+ (а+4))²;

    Випадки розкладу на множники

16+(n-2)n(n+2)(n+4)=(n² + 2n- 4)² ;  

81+(n-3)n(n+3)(n+6)=(n² + 3n- 9)²; 

256+(n-4)n(n+4)(n+8)=(n² + 4n- 16)²;

k⁴+(n-k)n(n+k)(n+2k)=(n² + kn- k²)²; 

В) многочлен (х - а₁)²(х - а₂)²(х - а₂)² … (х -  а_n)² + 1 – незвідний, тобто не розкладається на многочлени меншого степеня;

Г) якщо р – просте число, то многочлен х^р – х – 1 – незвідний, тобто не розкладається на многочлени меншого степеня;

Д) якщо р – просте число, а – натуральне число, що не ділиться на р, то многочлен х^р – х – а – незвідний, тобто не розкладається на многочлени меншого степеня;

Є) будь-який многочлен з цілими коефіцієнтами можна записати як суму двох незвідних многочленів.

Тотожності.

1=0,25(m²+1)²-0,25(m²-1)²  

 m=(m+0,25)²-(m-0,25)²

1 =  ? подумайте над власною формулою?   

  m = ? подумайте над власною формулою?         

m²=0,25(m²-1)²+0,25(m²+1)²   

m²=0,25(m²+1)²-0,25(m²-1)²

m² = ? подумайте над власною формулою?   

mⁿ = ? подумайте над власною формулою?        

mⁿ=0,25(mⁿ+1)²-0,25(mⁿ-1)²